Introduction
Overview
Jep is a Java library for parsing and evaluating mathematical expressions.
With this package you can take formulas as strings, and instantly evaluate
them. Many common mathematical functions and constants are built-in and ready
to use. But in addition, you can extend Jep with your own user defined variables,
constants, and functions.
Features
- Small size (only 281KB as jar archive)
- Fast evaluation
- Support for arbitrary-precision arithmetic
- Support for strings, vectors, and complex numbers
- Includes common math functions and predefined constants
- Supports Boolean expressions (!, &&, ||, <, >, !=, ==, >=,
and <=)
- Support for implicit multiplication (allows use of expressions such as
"3x" instead of "3*x")
- Support for assignment expressions (x = 5)
- Allows choice between declared and undeclared variables
- Extendable through user defined functions
- Customisable syntax for expressions
- J2SE 7 compatible
- Supports Unicode characters (including Greek symbols)
- Customizable error messages allow for Internationalization and localization
- Thread-safe evaluation
- Extensive documentation
- Includes JavaCC
grammar
Parsing and Evaluation
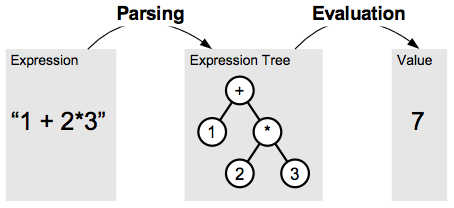
Evaluating a string expression with Jep is a two step process as shown in
the figure below. First the expression is parsed, bringing it from
a string representation into a tree representation. The tree
representation is a structured representation of the expression which allows
a simple and fast evaluation of the expression in a second step. The following
sections will discuss these two steps in more detail.
Parsing
One can describe parsing in general terms as taking a series
of characters as input and producing a structured representation of the information
contained in that set of characters. The focus here is on mathematical expressions
although parsing is also used for other areas such as natural language parsing
for example.
Math expressions can be represented by a tree data structure
where numbers, variables, operators and functions all are represented by nodes.
Numbers and variables are represented by so-called child nodes, while
operators and functions are represented by parent nodes. The parent
nodes operate on their child nodes. For example, the expression "1+2*3"
can be represented by a tree with five nodes, as shown above.
You might ask why the multiplication node is a child of the
plus node. The reason for this is operator precedence. Operators have
an order of precedence which needs to be obeyed when parsing expressions.
The precedence of multiplication is higher than that of addition. So, for
the above example, one needs to first multiply 2 and 3 before adding the result
to 1. In the tree, this is represented by grouping the the numbers 2 and 3
as children of the multiplication operator. Finally, the multiplication node
itself is a child of the addition node, expressing that the result of the
multiplication is used for the addition operation. The parser is responsible
for following the precedence order as specified in the grammar.
Parsers are typically generated using parser generators
such as JavaCC, ANTLR, SableCC, Yacc, or Bison. Some of the parsing routines
in Jep are generated using JavaCC (https://javacc.dev.java.net/).
Using a grammar defined in the JccParser.jjt file, JavaCC creates a set of
classes which perform the core tasks of the parsing process. A configurable pure java parser is also included.
Evaluation
Evaluation takes the expression from a tree representation to
the value of the expression. Since the tree is built according to the operator
precedence, the evaluation method does not need to know about operator precedence.
The tree can be traversed using a simple method to determine the value of
the expression.
A simple approach is to start from the root node (the
topmost node) and apply a recursive method. This can be implemented using
the visitor design pattern. A different method can be created for each node
type. To evaluate an operator or function node, first the child nodes are
evaluated. Then, using the values of the child nodes, the operator or function
is applied to determine the value of the node itself. For nodes that are constants
(numbers) or variables, the node evaluates to the value of the constant or
variable. Using such a recursive approach, the tree is quickly traversed in
a depth-first manner.
